
In the 1960’s the mathematician and meteorologist Edward Lorentz was attempting to simulate the behaviour of the atmosphere on a computer. At that time it was assumed that all that was needed to provide the perfect weather report was the right model and big enough computing grunt. Lorentz’s model for atmospheric convection consisted of the following three ordinary differential equations:
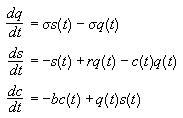
Now, these might look very simple equations, but due to the non-linear terms they cannot be solved analytically. A plot of the numerical values calculated from these equations using particular initial conditions is anything but simple, as can be seen from the picture above. Starting from any initial condition the calculations will approach the paths displayed in the image, but the actual path followed by the calculations is highly dependent on the initial conditions. The strange shape in the picture attracts points outside of it and as such is called an attractor.
If we were to magnify one of the lines in the shape we would see it was not just one line, but many. Continual magnification yields the same result, hence the shape is said to be self-similar. The lines map out an area of three dimensional space, yet don’t fill it. Yet, they also take up more room than a 2 dimensional surface. In fact, they have a dimension greater than two but less that three, a fractional dimension. These two properties define a shape called a fractal. An attractor with a fractal shape is called a strange attractor.
What Lorentz had shown was that the future state of the system was very sensitive to the initial conditions used for the calculation and hence even a deterministic system could be inherently unpredictable in the long-term. With reference to Lorentz’s strange attractor the famous statement on chaos says that the flapping of a butterfly’s wings in Tokyo can cause a tornado in Texas.