The Heisenberg uncertainty relates the uncertainties in position, ![]() , and in momentum,
, and in momentum, ![]() of a quantum particle in six dimensional phase space, such that each component of the position and momentum vectors satisfy
of a quantum particle in six dimensional phase space, such that each component of the position and momentum vectors satisfy
![]()
where h is Planck’s constant. In other words, the more localised a particle is, the greater the range of momentum it can possess. In other words, the particle will have a minimum average kinetic energy that will increase as the particle becomes more and more localised.
Another quantum mechanical factor is the Pauli Exclusion principle, which states that no two fermions (particles with a quantum spin of some odd multiple of 1/2) can be in the same state at the same time. If we consider an atom, this implies that only two electrons (spin 1/2) can occupy a given energy level, and they must have opposite spins.
Degeneracy occurs when all the fermions are in the lowest potential state. That is, when they are all in the lowest energy level configuration possible, arranged according to the Exclusion principle. The lower the energy state, the more localised the particle. Hence, from the Uncertainty principle, the greater it’s average momentum and kinetic energy.
The maximum momentum of a the particle in a degenerate state, at T=0 (so there is no translational momentum) is called the Fermi momentum and is given by the equation:
![]()
where n is the total number of particles per unit volume.
The energies of these particles may be relativistic. The relativistic total energy, and kinetic energy formulas are:
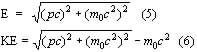
where m0 is the rest mass of the particle. If ![]() then it is said to be highly relativistic, or non relativistic is
then it is said to be highly relativistic, or non relativistic is ![]() . Also:
. Also:
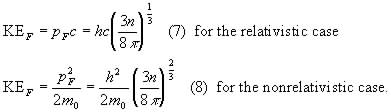
The relativistic aspects will play a larger role when considering neutron stars later.
It should be noted that the description for the completely degenerate gas does not include a reliance on temperature. From the general formula for the pressure of an isotropic gas:
![]()
The pressure P can be calculated. For a non-relativistic gas:
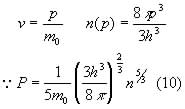
whereas for a fully relativistic gas:
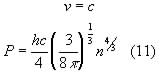
Neither of which are dependent on temperature.